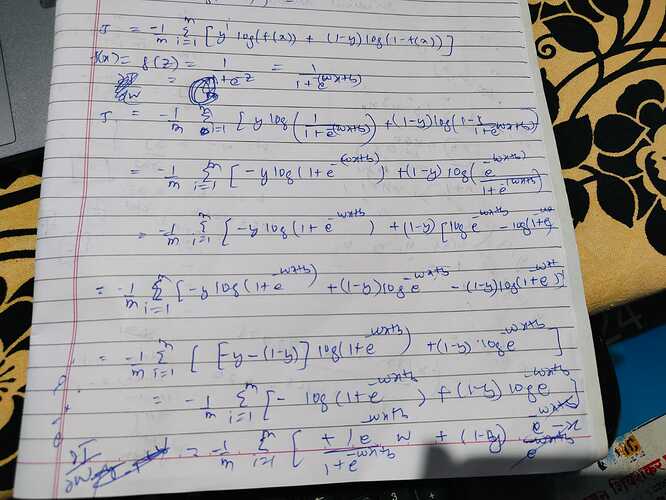Gradient Descent for logistic regression prrof

[HMDPatil]

Hello . I saw the gradient descent term for logistic regression , and I tried to derive the derivative term myself , but I think its quite different from whats shown in the course . Could anyone help ?

i have solved it in rough , but the last line is what i came up with . The issue is there is a ‘x’ term with(1-y) and there is also the exponential term in the numerator

[TMosh]

If you post your derivation, perhaps someone with a calculus background will comment on it.

[conscell]

Hi @HMDPatil

Model Setup
Input: x^{(i)} \in \mathbb{R}^n
Parameters: w \in \mathbb{R}^n, b \in \mathbb{R}
Label: y^{(i)} \in \{0, 1\}
Prediction: \displaystyle \hat{y}^{(i)} = \sigma(z^{(i)}) = \frac{1}{1 + e^{-z^{(i)}}}, where z^{(i)} = w^\top x^{(i)} + b, z^{(i)} \in \mathbb{R}

The loss for a single example is

\mathcal{L}^{(i)} = - y^{(i)} \log(\hat{y}^{(i)}) - (1 - y^{(i)}) \log(1 - \hat{y}^{(i)}).

The total cost over m examples:

J(w, b) = \frac{1}{m} \sum_{i=1}^m \mathcal{L}^{(i)}.

Let’s first compute \displaystyle \frac{\partial \mathcal{L}^{(i)}}{\partial z^{(i)}}. Since \hat{y}^{(i)} = \sigma(z^{(i)}), and using the identity \displaystyle \frac{d\sigma(z)}{dz} = \sigma(z)(1 - \sigma(z)), we have

\begin{align} \frac{\partial\mathcal{L}^{(i)}}{\partial z^{(i)}} & = \frac{\partial\mathcal{L}^{(i)}}{\partial \hat{y}^{(i)}} \frac{\partial \hat{y}^{(i)}}{\partial z^{(i)}} \\ &= \left( -\frac{y^{(i)}}{\hat{y}^{(i)}} + \frac{1 - y^{(i)}}{1 - \hat{y}^{(i)}} \right) \hat{y}^{(i)} (1 - \hat{y}^{(i)})\\ & = - y^{(i)} + y^{(i)} \hat{y}^{(i)} + \hat{y}^{(i)} - y^{(i)} \hat{y}^{(i)} \\ & = \hat{y}^{(i)} - y^{(i)}. \end{align}

Note that \displaystyle z^{(i)} = w^\top x^{(i)} + b = \sum_k w_k x_k^{(i)} + b, therefore

\frac{\partial z^{(i)}}{\partial w_j} = \sum_k \frac{\partial}{\partial w_j} w_k x_k^{(i)} = x_j^{(i)} \ \Longrightarrow\ \frac{\partial z^{(i)}}{\partial w} = x^{(i)}.

Using the chain rule:

\begin{align} \frac{\partial \mathcal{L}^{(i)}}{\partial w} & = \frac{\partial \mathcal{L}^{(i)}}{\partial z^{(i)}} \frac{\partial z^{(i)}}{\partial w} = (\hat{y}^{(i)} - y^{(i)}) x^{(i)}, \\ \frac{\partial \mathcal{L}^{(i)}}{\partial b} & = \frac{\partial \mathcal{L}^{(i)}}{\partial z^{(i)}} \frac{\partial z^{(i)}}{\partial b} = \hat{y}^{(i)} - y^{(i)} \end{align}

For the cost function is true

\frac{\partial J}{\partial w} = \frac{1}{m} \sum_{i=1}^m \frac{\partial \mathcal{L}^{(i)}}{\partial w} = \frac{1}{m} \sum_{i=1}^m (\hat{y}^{(i)} - y^{(i)}) x^{(i)},

\frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^m \frac{\partial \mathcal{L}^{(i)}}{\partial b} = \frac{1}{m} \sum_{i=1}^m (\hat{y}^{(i)} - y^{(i)}).

[HMDPatil]

Added

[HMDPatil]

Thanks .got it