In the Lab 4, the following quiver plot is generated.
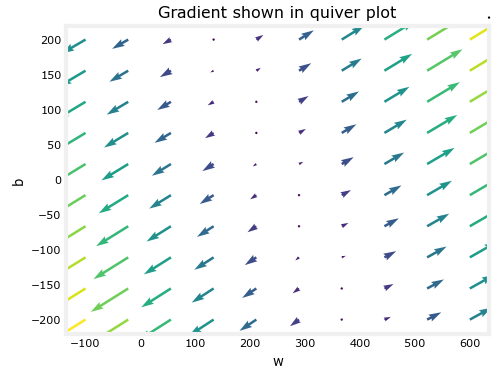
From this plot, we can identify the pairs of values for w and b that can bring the result of J close to 0, or the global minimum.
So why can’t we minimize J using the values we have for this plot? We can write a function that goes through the arrays corresponding to x and y values and choose the pairs that form the arrows with the smallest size.
So, instead of that, why do we write a separate function to implement gradient descent?
I’m a stranger to this field of maths and to ML. So my understanding could be very flawed.
Thanks in advance.
Hello @Govarthenan_Rajadura,
Yes, we can, in that particular case.
However, we learn gradient descent for a larger goal - cases where it will be computationally too expensive to make that plot such as a deep neural network which has way way way more trainable parameters (your example has only 2 trainable parameters - w and b).
So, in these courses, we learn gradient descent and we practice it with some simple case even though gradient descent is not absolutely needed. With these simple cases, learners can easily experiment and observe to clear for themselves doubt that they might have about how gradient descent works. Once they are familar with the concept of gradient descent and how gradient descent learns trainable parameters in simple cases, they are ready to move on to some less simple cases.
Cheers,
Raymond
1 Like
