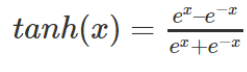A quick ChatGPT produce this tanh derivative calculation:
As
\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
Let y = \tanh(x). So,
y = \frac{e^x - e^{-x}}{e^x + e^{-x}}
Now, denote u = e^x and v = e^{-x}. Thus,
y = \frac{u - v}{u + v}
Then, using the quotient rule, the derivative of y with respect to x can be calculated as follows:
\frac{dy}{dx} = \frac{(v \cdot u' - u \cdot v')}{(v + u)^2}
Where ( u') and ( v' ) are the derivatives of ( u ) and ( v ) with respect to ( x), respectively.
u' = e^x
v' = -e^{-x}
Substitute these into the formula:
\frac{dy}{dx} = \frac{(e^{-x} \cdot e^x - e^x \cdot (-e^{-x}))}{(e^{-x} + e^x)^2}
\frac{dy}{dx} = \frac{(e^{x-x} + e^{x-x})}{(e^x + e^{-x})^2}
As e^0 = 1
\frac{dy}{dx} = \frac{1+1}{(e^x + e^{-x})^2}
\frac{dy}{dx} = \frac{2}{(e^x + e^{-x})^2}
Since {e^x + e^{-x}} = 2cosh(x), where cosh(x) is the hyperbolic cosine function, we can substitute this back:
\frac{dy}{dx} = \frac{2}{(2\cosh(x))^2}
\frac{dy}{dx} = \frac{1}{\cosh^2(x)}
\frac{dy}{dx} = \text{sech}^2(x)
And \text{sech}^2(x) is equal to 1 - \text{tanh}^2(x).