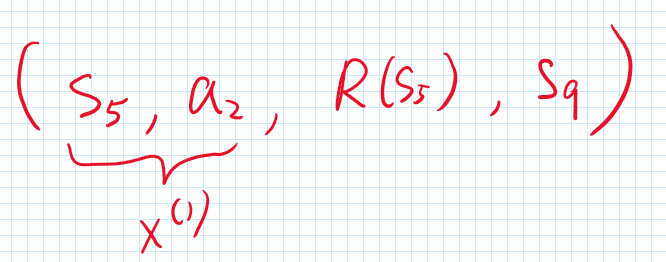When we are building the training set for the neural network on bellman equation, we will use the first 2 component to compute input X and the second 2 components will be used to compute output Y as shown in the image. But comparing the right side of the bellman equation and these second 2 components, i wonder how we compute max Q(S1 prime,A prime) from S1 prime?
Hello, @flyunicorn,
Verbally, it is just to substitute s'^{(1)} into Q, which makes Q(s=s'^{(1)}, a), and then try all possible values of a and pick the a=a' that maximizes Q, which makes it  .
.
You will find a practical example in the week’s assignment as you will be training a neural network.
Cheers,
Raymond
So it has nothing to do with s'^{(2)}? When Andrew was explaining on this slide, he circled the s'^{(2)} below and said that’s a state you got to in this example when he was explaining the first traning example, so I was confused how s'^{(2)} is relevant since we get y^{(1)} by trying all possible a' and pick the a' that maximizes Q(s',a')
We don’t use s'^{(2)} for getting y^{(1)}. I think it would be better to watch that lesson starting from 7:28 again, because Andrew said
There are four elements in this first tuple. The first two will be used to compute x^1, and the second two would be used to compute y^1.
and for “the second two”, they don’t include s'^{(2)}.
Cheers,
Raymond
Then what does Andrew mean when he says “that’s a state you got to in this example.” The whole paragraph he said is below. He said that sentence while he circled S’2
“Notice that these two elements of the tuple on the right give you enough information to compute this. You know what is R of S^1? That’s the reward you’ve saved the way here. Plus the discount factor gamma times max over all actions, a’ of Q of S’^1, that’s a state you got to in this example, and then take the maximum over all possible actions, a’. I’m going to call this y^1.”
Thanks for clarifying, @flyunicorn, I think s'{(2)} shouldn’t have been circled. At that time, if we listen carefully, Andrew was saying s'{(1)}.
The course team will be notified of this. Thanks @flyunicorn ![]()
Cheers,
Raymond
Thanks Raymond for the comments!
I think the obstacle that prevents me from understanding the DQN algorithm is that how could the initial guess of Q be improved to be the right number of Q, which is the output of the neural network. In supervised learning, we learned that the initial guess of parameters will produce an estimate y which we use to compare with the true y. Through minimizing the gap between estimate y and true y, then we improve parameters and finally produce estimate y as close as the true y. But in DQN algorithm here, when we have initial guess of Q which is like the estimate y, we don’t know the true Q which is the true y. Then how do we improve the estimate y? I’m very lost in this 16 minutes learning the state-value function video.
Hello @flyunicorn,
Yes, I know it might sound confusing to use the output from a randomly initialized Q network for part of the label to improve the Q network itself.

I think the first step to get away from this confusion is that we don’t focus on the second term but we focus on the first term because it is a piece of truth we inject to the network during the training process. With this, we know something true is being used to improve the Q.
Then the second step would be not to fix our eyes on one training example, but more. I will use two here:
Let’s say we have the following tuple to create (x^{(1)}, y^{(1)}):
and with that we compute the following label, assuming that a_3 is the best action:
Now, you might think this label y^{(1)} is bad because you don’t trust Q(s_9, a_3). However, what if I tell you a piece of new fact that the Q-network had been trained with the following example (x^{(0)}, y^{(0)}):
Would this piece of new information give you a little more confidence on the label y^{(1)}? Because in this case, (if the network had learned (x^{(0)}, y^{(0)}) perfectly) we can substitute y^{(0)} into y^{(1)} and we have:
Now, I will say y^{(1)} looks better than before because even though I may not trust Q(s_{21}, a_7), its significance has been dampened by gamma squared. You know, gamma is between 0 and 1 and when you square it, it’s only going to be smaller.
If you repeat this thought process for n times, you can imagine that the untrustworthy Q get diminished by \gamma^n.
The idea here is that, you won’t expect any major improvement in the first few rounds of training, but after some rounds, the previously trained example (like y^{(0)}) will kick in and make new example’s label (like y^{(1)}) better.
Therefore, two take-aways for how to get away from the confusion:

- remember we have the first term (the reward) which is a piece of true information.
- don’t stare at just one training example, but think about how previous examples and gamma can help.
Cheers,
Raymond
Not really, because Q(s9,a3) is a guess too.
But I sort of see where you are going. Because the second term is the best outcome of all sequential future states, we can write them all out one after another until we reach the terminal state. In this way, all the components in the Q function will be R(s1)+rR(s2)+r^2R(s3)+…+R^n*R(terminal state). Then, all components will be the truth because we already know R(s1) to R(terminal state). In this way, we have some truth to compare agaist the estimate Q. Is my understanding correct?
This I will agree with at first glance of y^{(0)}, but thing changes after the substitution of it into y^{(1)}, which you have seen it ![]()
![]()
I think your explanation is fine, but just one more point that, in the thought process, although you can, you don’t really have to go all the way to the terminal state, because with large enough n, \gamma^n can effectively kill the untrustworthy term. This is also how we can appreciate gamma.
This also means that you don’t have to have visited the terminal state (for drawing some training examples of that) to start to see the Q network performing better at states far away from the terminal.
Cheers,
Raymond