Why update all weights in the neural network with gradient descent? When you update the weights in the first layer the partial derivative of the next layer’s weights are included in calculation. Then you should only update the weights in the first layer. If no, why not.
Hello @Y_L1,
I don’t get the full picture of your reasoning. I believe you agree that all neural networks’ weights should be learnt. Let’s say we have a 3-layer NN, if we just update the first layer, how can the second and the third layer learn? Since we always randomly initialize all of the weights. If the second and the third layer don’t learn, will they remain randomized values forever?
I think thinking about these questions will help us move forward later.
Raymond
For the next layers the weights are the same but the variables change. So the activation value changes.
Alright, so if the weights in the 2nd and the 3rd layers are initialized randomly, then they remain randomized values forever.
Then let’s do an experiement to see some differences:
import random
import numpy as np
import tensorflow as tf
from sklearn.datasets import load_breast_cancer
def set_seed(seed=100):
np.random.seed(seed)
random.seed(seed)
tf.random.set_seed(seed)
X, y = load_breast_cancer(return_X_y=True)
X = (X - X.mean(axis=0, keepdims=True))/X.std(axis=0, keepdims=True)
set_seed(seed=100)
m1 = tf.keras.Sequential([
tf.keras.layers.Dense(16, activation='relu'),
tf.keras.layers.Dense( 8, activation='relu'),
tf.keras.layers.Dense( 1, activation='sigmoid'),
])
m1.compile(loss='binary_crossentropy', optimizer='adam')
m2 = tf.keras.Sequential([
tf.keras.layers.Dense(16, activation='relu'),
tf.keras.layers.Dense( 8, activation='relu'),
tf.keras.layers.Dense( 1, activation='sigmoid'),
])
m2.layers[1].trainable = False
m2.layers[2].trainable = False
m2.compile(loss='binary_crossentropy', optimizer='adam')
hists = {name: m.fit(X, y, batch_size=32, epochs=100, verbose=0) for name, m in {'m1':m1, 'm2':m2}.items()}
from matplotlib import pyplot as plt
fig, ax = plt.subplots(1, 1, figsize=(5,3))
for name, hist in hists.items():
ax.plot(hist.history['loss'], label=name)
plt.legend()
plt.show()
Here is the result
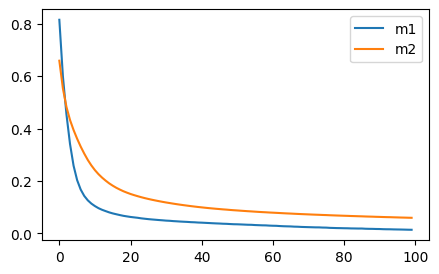
It doesn’t seem like freezing all but the first layer is bringing us benefit, does it? At least when the layers are randomly initialized, right?
Cheers,
Raymond