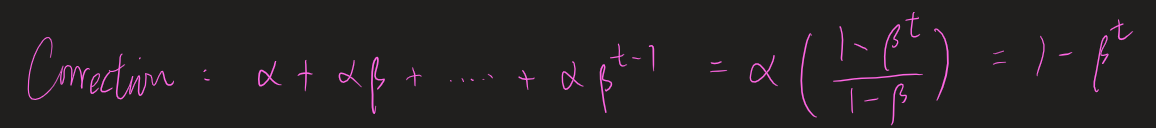Instead of the bias correction of dividing by 1-b^t, why can’t you just initialize the first v_0 to be \theta_0 * (1-b)?
Hi @Maxwell_Shapiro, I was also intrigued by the bias correction. Let me share what I found.
Let’s assume the data sequence: \theta_1, \theta_2, ..., \theta_t.
The Exponentially Weighted Average (EWA) is defined as follows:
EWA_\beta(\theta_1,...,\theta_t) = \frac{(\beta^{t-1}\theta_1 + \beta^{t-2}\theta_2 + ... + \beta^0\theta_t)}{\beta^{t-1}+\beta^{t-2}+...+ \beta^0}, 0 < \beta < 1
The denominator is a geometric series and we can simplify the equation:
EWA_\beta(\theta_1,...,\theta_t) = \frac{(\beta^{t-1}\theta_1 + \beta^{t-2}\theta_2 + ... + \beta^0\theta_t)}{\frac{1-\beta^t}{1-\beta}}
and
EWA_\beta(\theta_1,...,\theta_t) = \frac{(1-\beta)(\beta^{t-1}\theta_1 + \beta^{t-2}\theta_2 + ... + \beta^0\theta_t)}{1-\beta^t}
Note that the numerator is the definition of V_t and the denominator is the bias correction.
In other words, V_t is a very good approximation of EWA when t is large (\beta^t \rightarrow 0). However, when t is small (at the beginning of the series or iterations), we need the bias correction to make V_t the exact definition of EWA.
I hope this helps.
Hello @ViridianaL,
That’s interesting! Your \beta^0 term caught my eye because I wondered whether such term is possible (indeed it should be there), so I did a quick verify myself.
Here it is:
Note that v_0 =\theta_0 is initialized, and the rest of the \theta_t are obtained in the training process. Just to check, with the above, when t=1, v_1 = \beta v_0 + (1-\beta) \theta_1.
I am thinking maybe the correction term meant to ignore the last term of the sum in the second line of my above steps because it is “initialized”, so the correction becomes:
Since we are ignoring the last term in the second line of my above steps by setting v_0 = \theta_0 = 0, the coefficients no longer sum to 1, but the following:
where the \beta^t in the (1-\beta^t) is the term that we have ignored, and thus the correction.
If not ignored, it will become 1-\beta^{t+1} by arguing that v_0 = \alpha \theta_0 instead. (This is totally wrong)
Not sure if anything here makes sense, and not sure how correct this is as a math interpretation of the correction term, but probably not going to find out anytime soon, so don’t take this seriously.
Cheers,
Raymond
Hi @rmwkwok ,
Thanks for your comment. I believe we agree that the bias correction is for the case where v_0=0. The part I’m confused is to talk about \theta_0. We don’t have it because the data consists of \theta_1, \theta_2, ..., \theta_t, and it is ok because we provide an initial value to v_0. I’m wondering if I’m missing something.
Best,
Viridiana
Hey Viridiana @ViridianaL,
Indeed, it is set to zero. I edited my post.
You did not miss anything. My \theta_0 is just another name for v_0.
Thanks for your helpful post, and because of it, I got to go through this exercise and gained some interesting insight. ![]()
![]()
Cheers,
Raymond
Thanks for your answer. I feel, however, that I was not clear in my question:
In the video, Andrew had mentioned that the bias correction was primarily needed because we initialized v_0=0. My main question then becomes, why not initialize v_0=\theta_0 (initialize v_0 to be whichever is the first data point) and then iterate from there? In this way, for EWA, we needn’t bother with a bias correction. I mean, in your answer itself you state, “Let’s assume the data sequence: \theta_1,...,\theta_t”…
Perhaps I am not thinking this through well enough.