I’m trying to develop my intuition about the consequences of using separable convolutions vs traditional convolutions, but I’m not sure if my thinking is correct.
Traditional Convolution
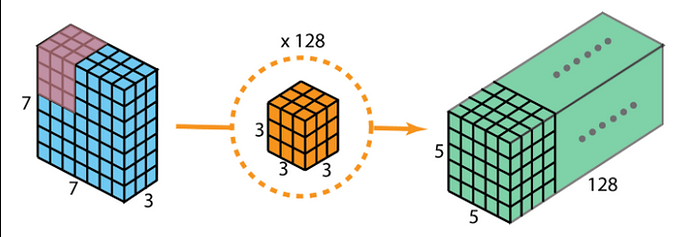
Consider a 7x7 pixel RGB image (n_H, n_W, n_C) = (7,7,3). We want to convolve it with a kernel (group of filters) of shape (f_H, f_W, n_C) = (3,3,3).
We can think of each (f_H, f_W) slice as a single filter that will be applied to one of the image’s RGB channels. During the convolution, each (3,3) filter is slid across one of the (7,7) image channels, the 9 weights are multiplied by 9 pixel values at each position, and their products are summed along the (H,W) dimensions, creating an intermediate (5,5,3) volume (tensor). Then, the values of that output are summed along the channel dimension so that we end up with a (5,5,1) output of the convolution.
The 27 parameters in the kernel are trainable, and during backprop, they are optimized until a useful filter is obtained. In practice, each kernel is an unknown linear combination of all possible filters, but for the sake of argument let’s say that one (3,3,3) kernel is optimized during training to a vertical-edge-finding filter:
\begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \\ \end{bmatrix}
This (3,3) filter is stacked 3 times to form a (3,3,3) vertical-edge-finding kernel.
If we want our network to recognize 128 features, we randomly initialize 128 (3,3,3) kernels, convolve each of them with the (7,7,3) image, and concatenate all convolution outputs so that we have a (5,5,128) tensor (volume), which becomes the input to the next layer.
We can think of each (3,3,3) kernel in our \left(3,3, \;3 \cdot 128 \right) kernel volume as a filter for an image feature: vertical edge, horizontal edge, diagonal edge, brightness gradient, etc. Many of these filters have different topologies, which can all be learned during backprop because each kernel is independently convolved with the image.
\begin{matrix} {\begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \\ \end{bmatrix}}& {\begin{bmatrix} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \\ \end{bmatrix}}& {\begin{bmatrix} -1 & -1 & 0 \\ -1 & 0 & 1 \\ 0& 1 & 1 \\ \end{bmatrix}} \\ vertical & horizontal & diagonal \\ \end{matrix}
Separable Convolution
The separable convolution is done in 4 steps:
- Perform a depthwise convolution of an (n_H, n_W, n_C) image with n_C ~~ (f_H, f_W) filters
- Batch-norm the result and perform a ReLU activation
- Perform a pointwise convolution of the (\_,\_,n_C) depthwise output with a (1,1,n_C) projection kernel
- Batch-norm the result and perform a ReLU activation
Steps 2 and 4 don’t impact the separable convolution intuition, so I’m ignoring them.
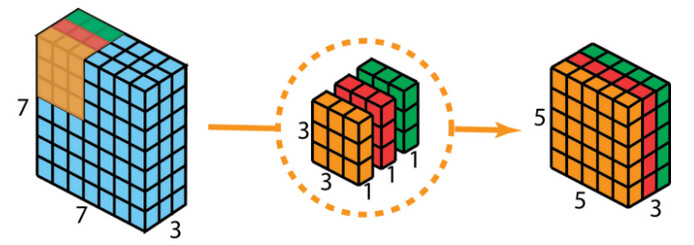
Step 1 - Depthwise Convolution:
Each channel of a (7,7,3) RGB image is convolved with one of a trio of (3,3) filters, but because we’ve separated the (3,3,3) kernel into three (3,3) filters, the 3 multiplication products at each pixel location CANNOT be summed along the channel dimension, since each individual filter has only 1 channel.
Aside: We’re still applying (3,3,3) \rightarrow 27 parameters to the image, but because we aren’t summing the products, the operation is not a traditional convolution; however, if we separate the (3,3,3) kernel into 3 \times (3,3) filters, we can still use the traditional convolution operation.
Ultimately the depthwise convolution gives us a (5,5,3) output, not the (5,5,1) output of a traditional convolution.
The 9 parameters in each of the 3 filters are trainable, and during backprop, they are optimized until a useful filter is obtained. In practice, each filter is an unknown linear combination of all possible filters, but for the sake of argument let’s say that each (3,3) filter is optimized during training to a vertical-edge-finding filter:
\begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \\ \end{bmatrix}
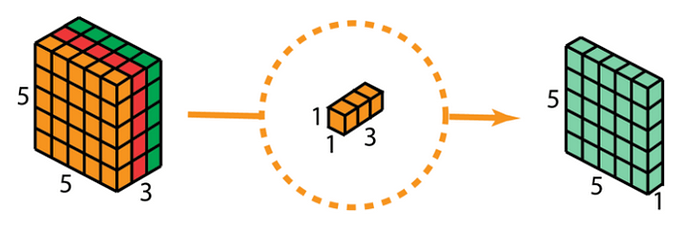
Step 3 - Pointwise Convolution:
The (5,5,3) depthwise tensor (volume) is convolved with a (1,1,3) projection kernel. During this convolution, at each pixel location, the 3 values are summed along the channel dimension, generating a (5,5,1) output.
The 3 parameters of the projection kernel are trainable, and during backprop, they are optimized until they represent the strength with which a filter should be applied to a channel. For example, if all 3 filters are trained to be vertical-edge-finders, and the projection kernel is trained to have the following values
\begin{matrix} {\begin{bmatrix} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \\ \end{bmatrix}}& & {\begin{bmatrix} 0.8 & 0.1 & 0.2 \\ \end{bmatrix}} \\ spatial ~~ filters & & projection ~~ kernel \\ \end{matrix}
It would suggest that important vertical edges are abundant in the red channels of the training images and relatively absent from the green and blue channels.
If we want our network to recognize 128 features, we randomly initialize 128 (1,1,3) projection kernels, convolve each of them with the (5,5,3) depthwise tensor, and concatenate all the resulting (5,5,1) pointwise tensors so that we have a (5,5,128), which becomes the input to the next layer. Each (5,5,1) slice represents some spatial feature of the image.
The Problem
In the traditional convolution example, We stacked 128 kernels and independently convolved each one with the input image, and I can see how this allows our network to learn 128 image features.With the separable convolution, we have only one set of filters, a single (3,3) for each RGB channel. This means that after convolving the (5,5,3) depthwise tensor with 128 \times (1,1,3) projection kernels, each (5,5,1) slice of the (5,5,128) output can only be a scalar multiple of the initial (3,3) filters. So it shouldn’t be possible for a MobileNet to learn orthogonal spatial features.
Example:
The depthwise convolution of some image’s red channel with a vertical-edge-finder should look something like this:
\underset{(7,7,1)}{I_{red}} \ast \underset{(3,3,1)}{F_{vert}} ~~ = \underset{(5,5,1)} {\begin{bmatrix} .010 & 31 & 33 & 30 & .016 \\ .014 & 33 & 32 & 32 & .011 \\ .011 & 33 & 33 & 31 & .014 \\ .011 & 30 & 31 & 34 & .012 \\ .012 & 32 & 31 & 33 & .013 \\ \end{bmatrix}} ~~ \approx ~~ {\begin{bmatrix} 0 & 30 & 30 & 30 & 0 \\ 0 & 30 & 30 & 30 & 0 \\ 0 & 30 & 30 & 30 & 0 \\ 0 & 30 & 30 & 30 & 0 \\ 0 & 30 & 30 & 30 & 0 \\ \end{bmatrix}}
For argument, assume that the blue and green channels also contain important vertical edges, so their vertical filters look roughly the same as the red channel’s.
When we convolve the (5,5,1) intermediate output with a (1,1,3) projection kernel, we first multiply the red (5,5,1) with the red parameter of the projection kernel, do the same for blue and green, then sum the results. The red multiplication is:
{\begin{bmatrix} .010 & 31 & 33 & 30 & .016 \\ .014 & 33 & 32 & 32 & .011 \\ .011 & 33 & 33 & 31 & .014 \\ .011 & 30 & 31 & 34 & .012 \\ .012 & 32 & 31 & 33 & .013 \\ \end{bmatrix}} \ast \underset{projection ~~ kernel}{\begin{bmatrix} {\color{red}0.50} & { \color{green}0.58} & { \color{blue}0.55} \\ \end{bmatrix}} ~~ = ~~ {\color{red}{\begin{bmatrix} .005 & 15.5 & 16.5 & 15 & .008 \\ .007 & 16.5 & 16 & 16 & .0055 \\ .0055 & 16.5 & 16.5 & 15.5 & .007 \\ .0055 & 15 & 15.5 & 17 & .006 \\ .006 & 16 & 15.5 & 16.5 & .0065 \\ \end{bmatrix}}} \\ \hspace{10.5cm}~~ \approx ~~ {\begin{bmatrix} 0 & 15 & 15 & 15 & 0 \\ 0 & 15 & 15 & 15 & 0 \\ 0 & 15 & 15 & 15 & 0 \\ 0 & 15 & 15 & 15 & 0 \\ 0 & 15 & 15 & 15 & 0 \\ \end{bmatrix}}
Multiplying a matrix by a scalar changes the magnitude of the values, but not the general topology. The blue and green parameters of the projection kernel are also close to 0.5, and the blue and green vertical filters are similar to the red filters, so when we do the blue and green multiplications, then sum everything up, we’ll get something close to
{\begin{bmatrix} 0 & 45 & 45 & 45 & 0 \\ 0 & 45 & 45 & 45 & 0 \\ 0 & 45 & 45 & 45 & 0 \\ 0 & 45 & 45 & 45 & 0 \\ 0 & 45 & 45 & 45 & 0 \\ \end{bmatrix}}
No matter the values in the projection kernel, because of our original vertical-edge filter, the pointwise convolution output will always have large values in the central columns and small values in the outside columns. Even if we stack up 128 projection kernels and optimize all their parameters during backprop, every (5,5,1) slice of our (5,5,128) layer output will look like this, just with different magnitudes in the central columns. As far as I can tell, one layer of a MobileNet can only learn one kind of spatial feature.
Here is the problem, a horizontal edge finder generates depthwise outputs that look like this:
\underset{(7,7,1)}{I_{red}} \ast \underset{horizontal ~~filter} {\begin{bmatrix} 1 & 1 & 1 \\ 0 & 0 & 0 \\ -1 & -1 & -1 \\ \end{bmatrix}} ~~ \approx ~~ {\begin{bmatrix} 0 & 0 & 0 & 0 & 0 \\ 30 & 30 & 30 & 30 & 30 \\ 30 & 30 & 30 & 30 & 30 \\ 30 & 30 & 30 & 30 & 30 \\ 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix}}
The horizontal-edge filter and depthwise matrix have fundamentally different topologies than those of the vertical-filter. If another training example contains horizontal edges, the parameters in the initial filters will be updated to reflect that, but the update will destroy the topology that made the vertical-edge-finder effective. Stacking projection kernels doesn’t solve the underlying problem. Adding more layers might help, by later layers won’t see the initial image, and any features that are orthogonal to the initial filter shouldn’t be propagated – the later layers won’t ever see them.
In practice, all parameters start out with random values, and the filter matrices don’t exhibit any strong topology. But, since the initial convolution layer can apparently only propagate a single feature, the network shouldn’t be able to learn any features very well.
Where is my intuition wrong? Can a separable convolution layer learn orthogonal or widely varying features? Are the feature relationships somehow expressed across multiple layers rather than one?