Simple BPTT for RNN implementation equation question

[Ted_Chou]

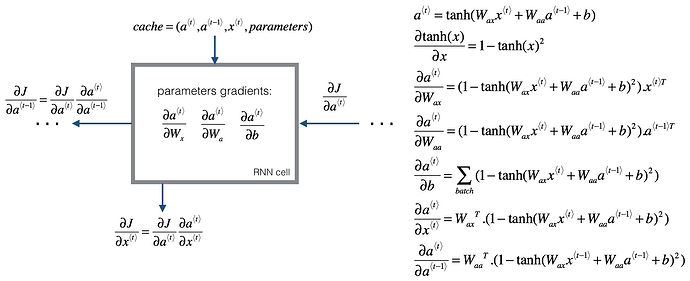
I am trying to implement simple RNN from scratch to understand the calculations step behind each implementation. Forward Propagation seems straightforward, but backward propagation seems very difficult. Especially the dimension does not match…

def rnn_forward(self, e) :
        for t in range(self.T_x - 1) :
            # single (n_x, n_m) m is training set size in time
            xt = self.cache['X'][:, :, t]
            # hidden state of previous step
            a_prev = self.cache['A'][:, :, t]
            # hidden state of next step is caculated by following weights and biases.
            a_next = tanh(np.dot(self.parameters['W_aa'], a_prev) + np.dot(self.parameters['W_ax'], xt) + self.parameters['b_a'])
            # using softmax as final activation
            yt_pred = softmax(np.dot(self.parameters['W_ya'], a_next) + self.parameters['b_y'])
            self.cache['A'][:, :, (t + 1)] = a_next
            self.cache['Y_pred'][:, :, t] = yt_pred

def rnn_backward(self, e):
        # cost function derivative
        self.cache['dY_pred'] = - (self.cache['Y'] / self.cache['Y_pred'])
        # initialized da
        da_next = np.zeros((self.n_a, self.m))
        for t in reversed(range(self.T_x - 1)) :
            # dimension seems to be (n_y, n_m)
            print(self.cache['dY_pred'][:, :, t].shape)
            # dimension seems to be (n_y, n_m) as well
            print(softmax_backward(np.dot(self.parameters['W_ya'], self.cache['A'][:, :, t]) + self.parameters['b_y']).shape)
            # following computation would have issues? da_prev is expected to have dim (n_a, n_m), but the dot of (n_y, n_m) and (n_y, n_m) don't give me (n_a, n_m)
            da_prev = np.dot(self.cache['dY_pred'][:, :, t], np.dot(self.parameters['W_ya'].T, softmax_backward(np.dot(self.parameters['W_ya'], self.cache['A'][:, :, t]) + self.parameters['b_y']))) + da_next
            self.cache['dW_ya'] += np.dot(self.cache['dY_pred'][:, :, t], np.dot(softmax_backward(np.dot(self.parameters['W_ya'], self.cache['A'][:, :, t]) + self.parameters['b_y']), self.cache['A'][:, :, t].T))
            self.cache['db_y'] += np.dot(self.cache['dY_pred'][:, :, t], softmax_backward(np.dot(self.parameters['Wya'], self.cache['A'][:, :, t]) + self.parameters['b_y']))
            self.cache['dW_aa'] += np.dot(da_prev, np.dot(tanh_backward(np.dot(self.parameters['W_aa'], self.cache['A'][:, :, (t - 1)]) + np.dot(self.parameters['W_ax'], self.cache['X'][:, :, t]) + self.parameters['b_a']), self.cache['A'][:, :, (t - 1)].T))
            self.cache['dW_ax'] += np.dot(da_prev, np.dot(tanh_backward(np.dot(self.parameters['W_aa'], self.cache['A'][:, :, (t - 1)]) + np.dot(self.parameters['W_ax'], self.cache['X'][:, :, t]) + self.parameters['b_a']), self.cache['X'][:, :, t].T))
            self.cache['db_a'] += np.dot(da_prev, tanh_backward(np.dot(self.parameters['W_aa'], self.cache['A'][:, :, (t - 1)]) + np.dot(self.parameters['W_ax'], self.cache['X'][:, :, t]) + self.parameters['b_a']))
            da_next = np.dot(da_prev, np.dot(self.parameters['W_aa'].T, tanh_backward(np.dot(self.parameters['W_aa'], self.cache['A'][:, :, (t - 1)]) + np.dot(self.parameters['W_ax'], self.cache['X'][:, :, t]) + self.parameters['b_a'])))

as the comment in the code, I can’t seem to implement the backprop correctly. The dimension doesn’t go together for da_prev to result in (n_a, n_m) correctly… Did I miss out on something?

Thank you!

[Ted_Chou]

Sorry, I left out some initialization part since those dont concern the question that much, but if you think those are essential, please do let me know.

[TMosh]

Are you attending the Deep Learning Specialization? This question appears to come from Course 5.

[paulinpaloalto]

@Ted_Chou

for t in range(self.T_x - 1) :

Are you sure that’s what you want? Note that python indexing (including ranges) is already “0-based”. I claim that means you will run one too few iterations. Try this and watch what happens:

for ii in range(5):
    print(f"ii = {ii}")

print(f"After loop ii = {ii}")

Tom’s point is the main one, though. This is covered in DLS C5 W1 A1, although they don’t really implement the complete back prop. But they do cover the part that you’re showing there.

[Ted_Chou]

Yes, thank you TMosh!
Yeap, it came from Course 5 W1.

But this image is all it had about differentiating. It only started half way, and it’s only with respect to da(t), not dJ (the cost function). Which is the part that I have some questions about.

paulinpaloalto
Thank you for the recommendation. I was spending most of my time understanding about the derivative part and took much less time in the validation part. I am still wondering about this part as well.
I want to have the indexing starting from 0, since my np matrices (self.cache[‘X’][:, :, t]) have indices 0. The self.T-x is a dimension, so the dimension number will be higher was my intuition for why to do -1. Let me look into this part as well.

[Ted_Chou]

So I was exploring this issue for the past few days. Seems like there are not a lot of examples of implementations online.
Especially about da and softmax derivative parts.
I made a simple script to see if the cost would reduce and it does indeed, let me post this and if you have advice or anything, feel free to comment:

import numpy as np
from utils import *
import random
import pprint
import copy
# from rnn import rnn
from rnn_utils import sigmoid, sigmoid_backward, relu, relu_backward, leaky_relu, leaky_relu_backward, tanh, tanh_backward, softmax, softmax_backward

x = np.array([[11, 25]]).T
a0 = np.array([[11, 10, 5.5, 3.5]]).T
Wya = np.array([[11, 15, 175, 21], [13, 12, 14, 150], [15, 7, 9, 1]])
Wax = np.array([[11, 15], [13, 12], [11, 3], [2, 5]])
Waa = np.array([[1, 1.5, 1.7, 2.1], [1.3, 1.2, 1.4, 1.5], [1.5, 0.7, 0.9, 0.1], [1.1, 1.3, 1.1, 0.3]])
ba = np.array([[10, 2, 5, 10]]).T
by = np.array([[10, 25, 1.5]]).T
y = np.array([[0, 0, 1]]).T

def forward(Waa, x, a0, ba, Wya, by) :
    a1 = tanh(np.dot(Waa, a0) + np.dot(Wax, x) + ba)
    y_pred = softmax(np.dot(Wya, a1) + by)

    return y_pred, a1
# print(L)

def backward(y, y_pred, da1, Waa, x, a0, a1, ba, Wya, by) :
    dy_pred = -y / y_pred
    dWya = dy_pred * np.dot(softmax_backward(np.dot(Wya, a1) + by), a1.T)
    dby = dy_pred * softmax_backward(np.dot(Wya, a1) + by)
    da1 = np.dot(Wya.T, dy_pred * softmax_backward(np.dot(Wya, a1) + by))
    # da1 = np.dot(Wya.T, dy_pred * softmax_backward(np.dot(Wya, a1) + by)) + np.dot(Waa.T, da1)
    dWaa = da1 * np.dot(tanh_backward(np.dot(Waa, a0) + np.dot(Wax, x) + ba), a0.T)
    dWax = da1 * np.dot(tanh_backward(np.dot(Waa, a0) + np.dot(Wax, x) + ba), x.T)
    dba = da1 * tanh_backward(np.dot(Waa, a0) + np.dot(Wax, x) + ba)

    return dWax, dWaa, dba, da1, dWya, dby

def loss(y, y_pred) :
    L = -y * np.log(y_pred)

    return np.squeeze(np.sum(L))


np.set_printoptions(suppress=True)
np.set_printoptions(precision=40)
counter = 0
da1 = np.array([[0, 0, 0, 0]]).T
learning_rate = 5000000
while counter < 1000000 :
    y_pred, a1 = forward(Waa, x, a0, ba, Wya, by)
    dWax, dWaa, dba, da1, dWya, dby = backward(y, y_pred, da1, Waa, x, a0, a1, ba, Wya, by)
    if counter // 100000 == counter / 100000 :
        # print(y_pred)
        print('%.30f' % loss(y, y_pred))
        # print(dby)
        # print(by)
        pass
    Wya = Wya - (dWya * learning_rate)
    by = by - (dby * learning_rate)
    # a1 = a1 - (da1 * learning_rate)
    Wax = Wax - (dWax * learning_rate)
    Waa = Waa - (dWaa * learning_rate)
    ba = ba - (dba * learning_rate)

    counter += 1

print(x)
print(a0)
print(Wya)
print(Wax)
print(Waa)
print(ba)
print(by)
print(y)

learning rate is either very big or it the cost reduces very slowly. It could be my implementation is still incorrect or the initial variables and weight matrices are too sporadic.

Anyways, if there are any masters do please guide me in the right direction.

Thank you.

[Ted_Chou]

this is a great page explaining how to simplify cross entropy to find the result of the softmax deriviative.

Cost function:
J = -y * log (y_pred)
y_pred = softmax(np.dot(Wya, a1) + by)

simplified:
dby = y - y_pred

broken down:
dy_pred = -y / pred
dby = softmax_backward(np.dot(Wya, a1) + by, dy_pred)

def softmax_backward(Z, dA):
    """
    Implement the backward propagation for a single softmax unit.

    Arguments:
    dA -- post-activation gradient, of any shape
    cache -- 'Z' where we store for computing backward propagation efficiently

    Returns:
    dZ -- Gradient of the cost with respect to Z
    """
    n, m = Z.shape
    A = softmax(Z).T
    tensor1 = np.einsum('ij,ik->ijk', A, A)
    tensor2 = np.einsum('ij,jk->ijk', A, np.eye(n, n))
    dSoftmax = tensor2 - tensor1
    dZ = np.einsum('ijk,ik->ij', dSoftmax, dA.T).T

    assert (dZ.shape == Z.shape)

    return dZ

ref: Softmax with cross-entropy
softmax_studies.xlsx.zip (12.8 KB)
softmax_studies.py (3.5 KB)