Hello,
I understood most of the video regarding the intuition of deriving the derivatives of trigonometric functions. My question is at 4:01 in the following link of the video:https://www.coursera.org/learn/machine-learning-calculus/lecture/CcD2l/derivative-of-trigonometric-functions
As delta x approaches 0, h becomes delta x and phi has a value of x. My question is how and why it is the case?
I’d appreciate an explanation. Thanks in advance.
Hi Ghinwa_Masri,
x is the angle expressed in radians, and delta x is a small increase in the angle also expressed in radians.
The radian relates to the length of a part of the circumference of the circle, as shown in this figure:
So a radian is both a measure of the angle and a measure of the circumference, and they correspond. For a circle with radius 1, the angle of a full circle - expressed in radiants - is 2 times pi and the full circumference is also 2 times pi. If the angle expressed in radiants is pi, the length of the circumference up to that angle is also pi. So if the angle expressed in radiants is delta x, the length of the circumference of that part of the circle is also delta x.
When delta x become smaller and smaller, the value of h in the triangle discussed in the video becomes more and more similar to the distance delta x along the circle.
As for the relationship between phi and x:
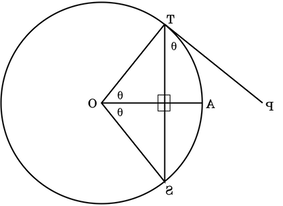
The tangent of a circle is perpendicular to the radius. Because of this, as delta x becomes smaller, phi approaches x, as shown in this figure in which x is represented by theta:
In a right triangle, the angles add up to pi. So at point T, the angle between the radius at angle x and the perpendicular is pi - 0.5*pi - x = 0.5*pi - x, and the angle between the perpendicular and the tangent equals 0.5*pi - (0.5*pi - x) = x.
I hope this clarifies.
