Week 4 exercise 6 decoderlayer (ed: potentially obsolete information from 2022)

[abelian_group_chen]

Test complained about the following line:

mult_attn_out2, attn_weights_block2 = self.mha2(query=mult_attn_out1, value=enc_output, key=enc_output, attention_mask=look_ahead_mask, return_attention_scores=True)

Do I need to subset the mult_attn_out1 to get Q? How would I actually do that if so? There has been no explanation on what Q/K/V actually mean and what values they contain other than the very brief intuition during lecture. I feel like even after this assignment I am not fully understanding Transformers beyond a very high level. Pedagogically, it would really help if we are given a baby example of what Q/K/V actually are. Right now with all the information given, including the original paper, little to no intuition can be gained. For example, I get feeding the same Q/K/V means self attention, but what does that actually mean and what is it doing? What does it mean to have query/key/value to be the same? It doesn’t make any sense in a database context so the lecture analogy falls apart.

[abelian_group_chen]

I’ve changed the attention_mask to the padding_mask and I am still getting the same error:

---

AssertionError Traceback (most recent call last)
in
1 # UNIT TEST
----> 2 DecoderLayer_test(DecoderLayer, create_look_ahead_mask)

~/work/W4A1/public_tests.py in DecoderLayer_test(target, create_look_ahead_mask)
179
180 assert np.allclose(attn_w_b1[0, 0, 1], [0.5271505, 0.47284946, 0.], atol=1e-2), “Wrong values in attn_w_b1. Check the call to self.mha1”
→ 181 assert np.allclose(attn_w_b2[0, 0, 1], [0.32048798, 0.390301, 0.28921106]), “Wrong values in attn_w_b2. Check the call to self.mha2”
182 assert np.allclose(out[0, 0], [-0.22109576, -1.5455486, 0.852692, 0.9139523]), “Wrong values in out”
183

AssertionError: Wrong values in attn_w_b2. Check the call to self.mha2

[anon57530071]

I believe that “query” is not output from the first MHA layer, but output from layer normalization. Please double check.

[anon57530071]

Pedagogically, it would really help if we are given a baby example of what Q/K/V actually are. Right now with all the information given, including the original paper, little to no intuition can be gained. For example, I get feeding the same Q/K/V means self attention, but what does that actually mean and what is it doing? What does it mean to have query/key/value to be the same?

Here is an overview of the first part of Decoder.

Inputs for the first MHA are query=X, value=X, and key=X, since we are creating “self-attention”.
In the 2nd MHA, it accepts inputs from Encoder (keys and values), and check the similarity with queries created by self-attention, the first MHA in Decoder.

Hope this helps some.

<Update : the last sentence about relationship among Q, K, V are updated.>

[TMosh]

@abelian_group_chen

I feel like even after this assignment I am not fully understanding Transformers beyond a very high level.

This is a very common feeling about this subject. There are some open tasks for the course staff to expand on this.

You may find more enlightenment from also studying the ungraded labs.

[abelian_group_chen]

I really appreciate the fast response and the high effort involved! This is great stuff in terms of helping to understand the dimensions inside the attention layer. I guess what still troubles me is I still can’t find a connection between what Andrew said in lecture and this assignment, i.e., Q being the query, for example q1= what happened there? q2 = did what there? k1 = person, k2 = action, v1 = Jane, v2 = visit, etc. From this assignment, it doesn’t seem like Q/K/V are anything like what was said in lecture since Q=K=V. If they are just generic tensor inputs to part of the network it would almost be better to just call them something generic like Q1/Q2/Q3 instead of trying to give them intuitive meaning like Q/K/V. The original paper doesn’t seem to explain much either on this front. What differentiates Q from K from V? From the embedding + positional encoding to Q/K/V, are some bits going into Q and other going into K? This is the part I am struggling with.

[TMosh]

I agree, the explanation in the lecture doesn’t match the actual practice. I find it confusing also.

There is an open request to make some improvements to this exercise.

[anon57530071]

Q, K, V structure is not an original technology of Transformer.
Simple “attention” mechanism uses a “Source-Target” type reference model. It only has a direct reference among “target” and “source” like the left-hand side chart below. (A diagram is from FRUSTRATINGLY SHORT ATTENTION SPANS IN NEURAL LANGUAGE MODELING.

But, this direct relationship may not be flexible if “these two are quite similar and should have relations, i.e., attention, but a referred word needs other word to be meaningful”. Then, “source” was separated into “key” and “value”, and “target” was renamed as “query”, just like the right-hand side chart. Later, this key-value pairs are called “dictionary”. Details are in Key-Value Memory Networks for Directly Reading Documents. (In the past work, K-V is also called “memory”.)

So, straightforward implementation of this Q,V,K system is “Source/Target attention”, which is the 2nd MHA in our assignment. In the case of English->French translation, “Source” is Encoder side which has “English” dictionary, and “Target” is Decoder that has French reference sentence (label).

In here,

Q : Target (output from 1st MHA in Decoder, French sentence)
K/V : Source (output from Encoder, English sentence)

(Note that “sentence” is not a list of word, of course. It is “word embedding” + “position encoding”.)
Then, create attention weights to translate English sentence to French sentence.

Now, let’s go to “Self-attention”. (I think starting from “Self-attention” may not be appropriate without having knowledge of Transformer overview.)
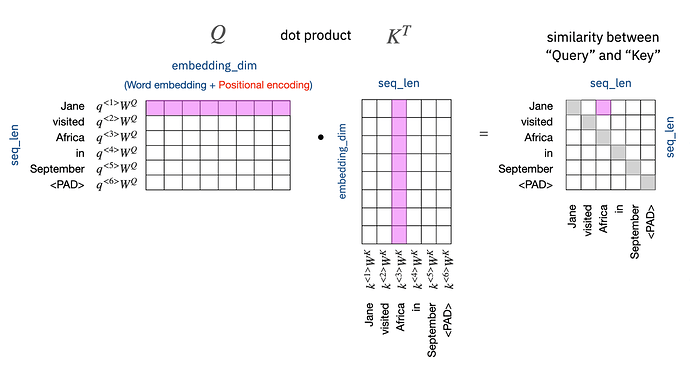
The first step in MHA for self-attention is to find similarity between Q (query) and K (key).

It is simply done by "dot product’. Remember that “dot product” is basically a “cosine similarity” from its definition.

a\cdot b = \parallel a\parallel \parallel b\parallel\cos\theta

If two vectors are similar, then, \cos\theta becomes close to 1. I suppose you remember “word embedding”. That’s I’m referring. This is one aspect of this MHA, but, think good for “intuitions”

With this, we can create a similarity map, which is a base for attention weights. The key point is that we Q (and K, V also), includes both “word embedding and position encoding”. If it is only “word embedding”, then a cosine similarity is just for a word itself, not including any position information. That’s not what “attention” expects. With adding 'Position encoding", then, we can define a similarity from both “word vector” and “word position” view points

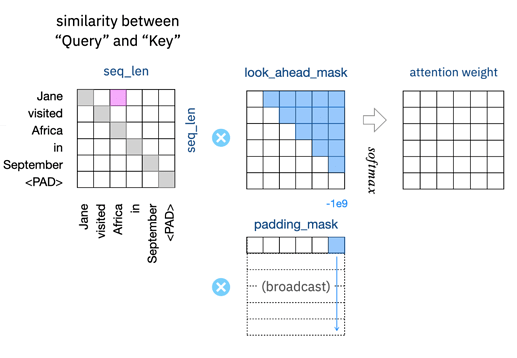
Then, we apply masks and create attention weights with Softmax (and some scale factors based on d_{model}, which is equal to “embedding_dim” in out case). Finally, we get the final output by a dot product of attention weights and V. Important thing is a mapping between k and v is also trainable.

Hope this helps some.

[abelian_group_chen]

Wow, this definitely clears up some of my earlier questions. Again I applaud you for such a high quality answer!

[TMosh]

@anon57530071, that’s terrific information. It plugs the knowledge gap in this exercise.
I’m going to submit a request to the course that it be included within the course material.

[Federico_Federales]

For those of us taking the course in '23 and '24, the code recommendations above are no longer valid. The variable order that passes the auto-grader actually correspond to the Tensorflow documentation, q/k/v instead of k/v/q. I could be misunderstanding but I spent a couple of hours going through docs and checking my answers and this is my conclusion now that I see, ‘All tests passed’!

[TMosh]

I’ve modified the thread title to warn about the information being obsolete.