Hello, since we have exactly 100 people, I assume there should not be any people with both headache and fever. Lets assume that 10 people have both headache and fever, then total number of people cannot be 100 since 50 + 50 - 10 = 90.
However, it is stated that there are 100 people. What am I thinking wrong? Can you explain this?
This is not a correct assumption.
Dear @Cagan_Yigit_Deliktas,
Your assumption is wrong, because if 10 people have both headache and fever, that means other 90 people may have headache or fever.
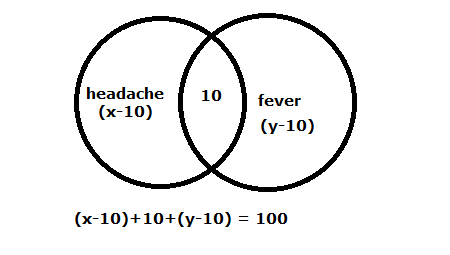
Hope this makes you clear.
According to your drawing, I think y should be 50 because it is said in the question that 50 people have fever and x should be 50 as there are 50 people with headache. When we sum these numbers up, we get (40 + 10 + 40) 90 people. I am sorry, I just could not understand the logic.
In my drawing, the only solution is a = 50, b = 0 and c = 50. There is no intersection. Can you explain what is wrong here?
Because you are assuming that 10 people have both headache and fever.
So intersection value should be 10.
I drew this without assuming the intersection is 10, just using the information given in the question. a + b = 50 because 50 people have headache, b + c = 50 for the people with fever and a + b + c = 100 since there are total of 100 people. Thus, b must be 0. What did I do wrong here? This is the last question ![]() sorry for asking too much
sorry for asking too much
your equation
a+b = 50 (correct)
b+c = 50 (correct)
but if your assumption is 10 people have both headache and fever, then the value of b should be 10.
Hope this makes you clear.
For my drawing, I did not assume the intersection is 10. I drew it just using the information given in the question.
Since a + b + c = 100, a + b = 50, b + c = 50, then b should be 0, right? What am I doing wrong here?
Then you are right. but these two sets are not disjoint.

