Incorrect variance computation in Regression Trees (optional)

[ai_is_cool]

Please can anyone comfirm that Prof. Ng has miscalculated the value of variance for the weights of animals in the earshape split?

Pointy ears have weights 7.2, 9.2, 9.4, 7.6, 10.2 for which he computes a variance of 1.47 but i compute this to be 1.29.

And floppy ears have weights of 8.8, 15.0, 11.0, 18.0, 20.0 for which he computes a variance of 21.87 but i compute this to be 17.49 using numpy.var(…).

Some of the other values for variance are wrong as well.

[paulinpaloalto]

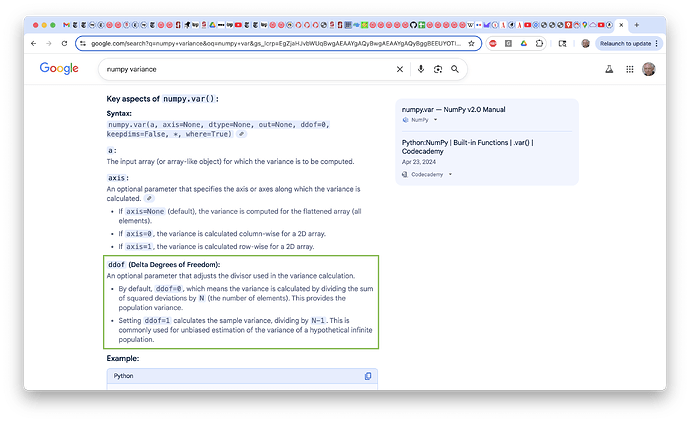
There are two ways to compute variance: the “population” variance or the “sample” variance. Here’s the google search output for numpy.var():

Here is some sample code:

a = np.array([7.2,9.2,9.4,7.6,10.2])
av0 = np.var(a)
print(f"av0 = {av0}")
av1 = np.var(a, ddof=1)
print(f"av1 = {av1}")
a = np.array([8.8,15.0,11.0,18.0,20.0])
av0 = np.var(a)
print(f"av0 = {av0}")
av1 = np.var(a, ddof=1)
print(f"av1 = {av1}")

Which produces the following output:

av0 = 1.2895999999999996
av1 = 1.6119999999999994
av0 = 17.4944
av1 = 21.868

I don’t have access to those lectures, but it does look like his computation for the pointy eared case differs from the above. Are you sure you copied those numbers correctly? But the numbers in the floppy ear case would be consistent with you using the default ddof = 0 and Professor Ng using ddof = 1. It might be worth a more careful look at what he said and see if he gives the formula using the factor of \frac {1}{n-1}.

[ai_is_cool]

I see, yes that would explain it.

Thanks.

[ai_is_cool]

Can you present a mathematical proof that sample variance is always smaller than population variance?

[paulinpaloalto]

No, sorry, statistics is not my field. But I would imagine that a google search would be able to find that for you.

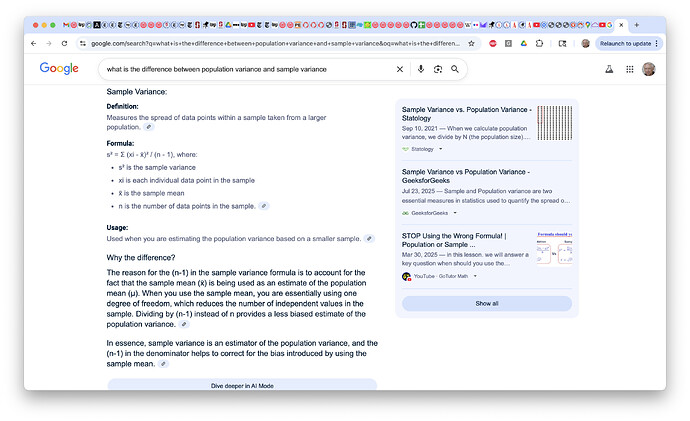
Here’s the most relevant part of the “AI search” answer from google search to the question “what is the difference between population variance and sample variance”:

I would be worth trying that yourself and reading all that it says. As you can also see on the RHS, it gave several links to articles on stats websites.

[ai_is_cool]

Thanks, ChatGPT has helped me.

[ai_is_cool]

Can anyone provide a proof that the expectation of the sample mean of a discrete distribution is equal to the population mean?

ChatGPT isn’t helping me very much.

Thanks