In the quiz that pops up, the question says what is country associated with Ankara (9,1) if we know that USA (5,6) & Washington DC(10,5).
To solve this we first get the difference of we get difference of USA & Washington and add it to Ankara. If we do that the country representation that we for Ankara is (4,2). And if we get the Euclidean distance it 5.09.
But in the solution it says it is Turkey with a Euclidean distance of 1.41.
Can someone please tell me how we arrive at this 1.41?
Hi @Girish_Garg
The question is:
Use the method presented in the previous slide to predict which is the country whose capital is Ankara.
So you use cosine similarity for prediction:
# Cosine similarity: country (4, 2); Turkey(3, 1) = 0.9899
(4*3 + 2*1) / ((4**2 + 2**2)**0.5 * (3**2 + 1**2)**0.5)
# Cosine similarity: country (4, 2); Japan(4, 3) = 0.9839
(4*4 + 2*3) / ((4**2 + 2**2)**0.5 * (4**2 + 3**2)**0.5)
The second part is Euclidean distance from point (4, 2) to (3, 1):
d = ((4-3)**2 + (2-1)**2)**0.5 # which is: 1.41
d = ((4-3)**2 + (2-1)**2)**0.5 # whichs is: 1.41
Hi @greedycat
Is that a question? But just in case I will elaborate:
Euclidean distance is calculated by:

The city distance we are trying to measure is from this plot:
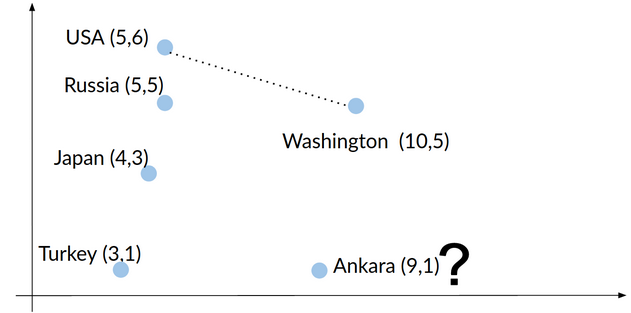
In this case, point A is a missing country - there is no country in exact point (4, 2).
In case your wonder, we get (4, 2) by using the difference vector “diff”: USA(5, 6) - Washington(10, 5) , which is (-5, 1). We use this diff vector to find the country from Ankara (9, 1) in this way Ankara + diff and we get (9-5, 1+1) = (4, 2).
Now the point B is Turkey(3, 1) - we found that it is the case by calculating cosine similarity.
So, point A is (4, 2), point B is (3, 1) and we plug these coordinates to the Euclidean distance formula above. \sqrt{(4-3)^2 + (2-1)^2} \approx 1.41
It’s not a question. In the formula you wrote, it should be ‘+’ instead of ‘-’.

