When creating a post, please add:
- Week # must be added in the tags option of the post.
- Link to the classroom item you are referring to:
- Description (include relevant info but please do not post solution code or your entire notebook)
Hi Course Team,
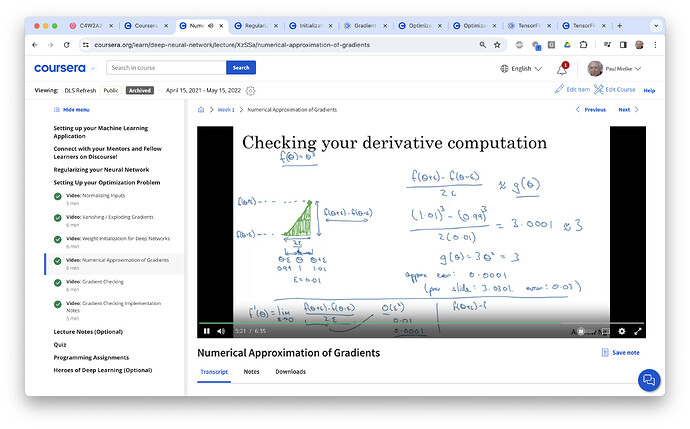
There is a small typo in the slide aound 2:43.
f(theta+epsilon) - f(theta-epsilon)/2epsilon ~ g(theta) (should by g’)
Numerical Approximation of Gradients | Coursera
I would say that if you’re going to change the formula in the upper right there, the RHS should be f'(\theta). Either that or use g() on the LHS as well. Which function are we talking about there? The general case f(\theta) or the specific example g(\theta) = \theta^3?
I will go back and listen to the words he says there and then will file a ticket to do some sort of fix.
As mentioned in the original post, the above slide is from the lecture Numerical Approximation of Gradients in DLS C2 W1. I went back and watched that again. Here’s what we have 2:43 into the lecture:
It’s a little unclear at that point what he means when he writes the formula in the upper right:
\displaystyle \frac {f(\theta + \epsilon) - f(\theta - \epsilon)}{2\epsilon} \approx g(\theta)
But if you look a bit later you see this as of 5:21:
So it becomes clear that he meant is g(\theta) = f'(\theta) = 3\theta^2. So the formula that is being referred to here in the upper right is actually correct.
If there is any clarification required here, it is that I’m pretty sure he never made that comment in the earlier part of the lecture as to what he means by g(\theta). The first time it appears it is in the form of a “forward reference”.
The bottom line here is that the slide as shown is correct, but you need to wait a bit to get the full context and understand what he is saying there.
Thanks for the clarification. I confused g(theta) with f(theta). g(theta) is actually f’(theta). And as you said, g was not mentioned up to that point. So, the slide is correct.