Query Computation in Self-Attention: Are Multiple Linear Transformations Redundant or Essential

[wallik2]

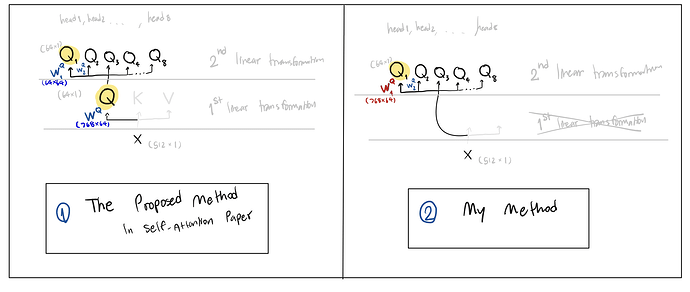
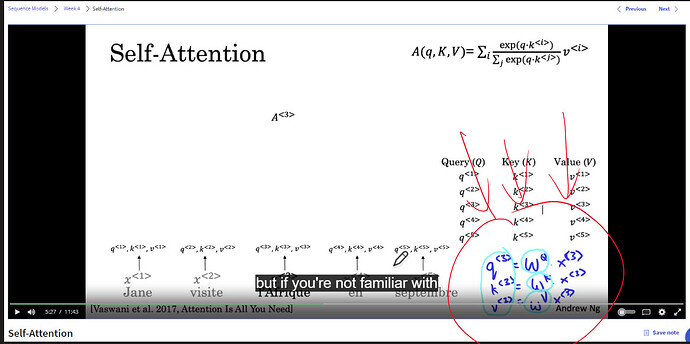
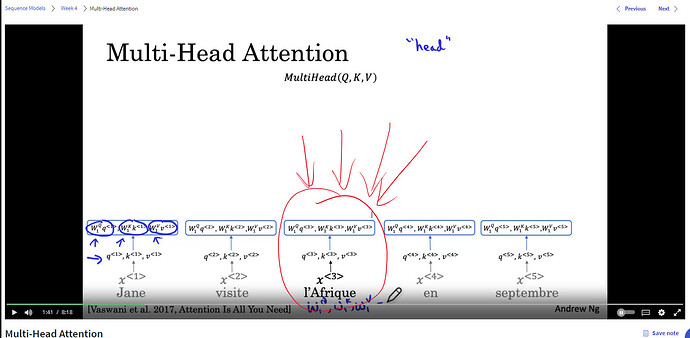
In the self-attention mechanism, when computing the query vectors (Q), why do we use separate linear transformations for each step (Q = dot(W^Q, X) and Q_1 = dot(W^Q_1, Q) instead of just using a single linear transformation (Q_1 = dot(W^Q_1, X))? Isn’t the first method still a linear transformation of X, which is equivalent to the second method? It seems redundant to have multiple linear transformations. What are the benefits or justifications for this approach?

The figure is shown below for better understanding what I’m trying to ask here (Assume the embedding dim = 512, and projection_vector_dim = 64)

If you are still struggling to grasp the concept of why the combination of two linear transformations resembles a single linear transformation, try to imagine a deep neural network operating without any activation functions

[rmwkwok]

Hello @wallik2,

Can you share the source (the link to the paper, then which page of the paper, then which paragraph/section /figure on that page) that gave you the idea that it worked as you described?

Raymond

[wallik2]

Here are two sources :

FIrst from Andrew NG slide

What I get from Andrew speech there is that

---

“First, we linearly mapping from X<1> to a set of queries, key, values” (Hence we employed the trainable weights for this mapping called W^Q, W^K, W^V)

So Q = W^Q • X, K = W^K • X, V = W^V • V

Now we also do another linearly mapping, so that each attention heads could have different queries, keys, value representation (Thus, we employed another trainable weights for this mapping called W^Q_i, W^K_i, W^V_i where i is head index)

---

Another source is Self Attention is all you need, I think the authors mentions this step here, Page 5, and the first paragraphs

Thank you for clarifying what if my understanding is wrong (like It’s not two repeated linear transformation because …)

[rmwkwok]

Hello @wallik2

But the problem is, from your last message, I don’t really see we are applying one linear transformation directly after another, without anything in between.

Can you at least tell me like: which one is that first linear transformation and which one is that second linear transformation?

I need to know exactly, in your understanding, which two steps are done in that way. I don’t see any two steps are done in that way and it becomes difficult for me to focus on exactly where might be any misunderstanding.

If it is not trivial to point out those two steps from the two sources, you might also check out the assignment of the week for transformer, because we are implementing that and if there are such two steps, then let me know, but I did take a quick look and I still couldn’t find case like that.

However, if you go to the assignment and find that the assignment is able to clear your doubt, then it is a very good result!

Cheers,
Raymond

[rmwkwok]

For example, for this pair of equations:

The Attention function has a softmax there, so it is a non-linear transformation. You will also implement that in the assignment. Is that the problem?

Raymond

[wallik2]

Thank you for your response

Here’s my clarification:

Let x → y represent y is a linear transformation of x

so,

The first linear transformation : input embedding X → Q

Now, recall that the Q is one of the input for every attention head right? but each attention head needs each query representation to be different, so we will apply another linear transformation

The second linear transformation : Q → Q_i (where i is i_th attention head)

Let me know if this still is not clear for you

[wallik2]

I’m sorry for not stating clear enough, I would like to focus on this equation where you can see that QW_i^Q is the second linear transformation

You also have noticed that the way we obtain Q is the first linear transformation of X

[rmwkwok]

Thank you @wallik2, I will check out the lecture videos again and try to put myself in your shoes, but that will be after I get to my laptop which probably will be an hour or so later. Let’s continue a bit later.

Cheers

Raymond

[rmwkwok]

@wallik2

Let me know if this is the problem.

In Course 5 Week 4 video “Self-Attention” at 5:27, in the bottom right corner, there is the first set of linear transformations.

In Course 5 Week 4 video “Multi-Head Attention” between 0:36 and 0:50, Andrew recalled (in narration) the above set of linear transformations which made you think that the q^{<3>}, k^{<3>}, v^{<3>} were also computed with that set of linear transformations.

Quoting the narration:

Remember that you got the vectors Q K and V for each of the input terms by multiplying them by a few matrices, W Q W K and W V. With multi head attention, you take that same set of query key and value vectors as inputs. So the q, k, v values written down here

Then at 1:41, we find q^{<3>}, k^{<3>}, v^{<3>} were linearly transformed again:

---

So,
from the first video, we had q^{<3>} = W^Qx^{<3>}
from the second video, we had W^Q_iq^{<3>}

and combined, we had two linear transformations one after another: W^Q_i \times W^Q \times x^{<3>}

and such consecutive linear transformation is, to you, redundant, and can be replaced by just one linear transformation, and you wanted to ask why we didn’t have just one linear transformation here.

---

I very much believe this is the problem, is this?

I am trying to make things very clear and explicit, as I have a feeling that we might want a few more people to have a look too. Anyway, before I continue, just let me know if this is the problem and if I have missed out anything.

[wallik2]

You are right, that was my question.

Although it might not be that big deal, since the performance of having one or two linear transformation is not that different.

But, in case we need to optimize the memory or time. So, It’s possible that we can replace

Q = W^Q_i x W^Q x X

by

Q = W^Q_i x X

[rmwkwok]

Hey @wallik2,

Thanks for confirming!

I want to first share my understanding , and then I will talk about the “confusion” due to the two videos as I illustrated in my previous post.

My understanding is that, the actual implementation is NOT like that we are doing W^Q_i \times W^Q \times x^{<3>}, instead it is doing W^Q_i \times q^{<3>} (where q^{<3>}= x^{<3>}) . What I am saying is that, in the actual implementation, we actually don’t have two linear transformations but just one, and we can see that in the assignment, in this tensorflow tutorial, and even after I read the “Attention is all you need” paper.

Seeing me say that there is just one linear transformation, I know you probably will ask immediately, then why the videos? Why the videos give us the idea that there are two consecutive linear transformations which is obviously redundant. Right now, at this moment, I am wondering if there is any problem with the videos, or if my interpreation (shared in my previous post) about the two videos are wrong - well, MAYBE the q^{<3>} in the 2nd video is not equal to the q^{<3>} from the first video. For this, I will need to invite other mentors for comments but that’s going to take time.

For now, I would like to share my understanding that I believe should also be observable from the assignment:

1. let’s say our query has only one word, e.g. “hello”
2. that “hello” get converted into a token, say x^{<1>} = 123
3. a token is converted into an embedding q^{<1>} = \text{a vector}
4. the query vector is multiplied to the W^Q_i in the i-th head, or W^Q_iq^{<1>}
5. similar steps for the key and the value k^{<1>}, v^{<1>}
6. then the Attention function that does the softmax thing.
7. so just one linear transformation.

So, you might choose to take my words (just one linear transformation), or stay how you are understanding it (two redundant linear transformations), or keep both in mind, and then see if there are comments from other people in the future.

Lastly, I just want to know that I am taking your question very seriously. Also, if there were really two linear transformations, then you were absolutely right that it is not necessary and will only cost more time.

Cheers,
Raymond

[rmwkwok]

Just why I think the “Attention is all you need” paper meant to have only one linear transformation.

On page 5,

we see that which implies that the last dimension of Q takes the size of d_{model}.

From page 3, let me quote,

d_{model} is the embedding size. The simplest way to understand these is that Q is a stack of embeddings, instead of a linear transformation of the embeddings which doesn’t change size.

[rmwkwok]

Hopefully this might further clarify, in my opinion, why there is the confusion.

I suppose the first video was based on the following equation on page 4

where Q, the query, is said to have dimension d_k in the following paragraph:

Then, I suppose the second video was based on the following equation on page 5

where Q actually has a DIFFERENT dimension, and it is d_{model}. Only QW_i^Q has a dimension of d_k.

Therefore, the same symbol Q has two different definitions and different shapes in the two equations, and if the videos were indeed based on those two equations, then the Q in the first video is not identical to the Q in the second video, and this justifies my following guess:

@rmwkwok

MAYBE the q^{<3>} in the 2nd video is not equal to the q^{<3>} from the first video

@wallik2, you mentioned that you came to the conclusion that there were 2 linear transformations after reading the paper, would my explanation above give you any new perspective?