When fitting the a model over 100 epochs with a ‘LearningRateScheduler’ as callback after each epoch, isn’t the loss for each epoch (with a new learning rate) being impacted by the parameters that have been learnt by the NN with those previously tried learning rates in previous epochs?
If this is the case, how is this a good way to determine a learning rate?
Would it be more appropriate to run a few epochs for for one specific learning rate and (while resetting parameters) iterate to get the loss after each of this process?
Question about optimizing the learning rate by fitting the NN with LearningRateScheduler as callback
Hello Rodolfo,
The reasoning behind 100 epochs is not only based on Learning rate only. It is combination of choosing the appropriate learning rate with the precise cost function and getting the best accuracy. So in some model epoch of 100 is required based on the custom loss, training model as mentioned by you the parameters.
A good way to determining a more precise learning rate is to choose the most random learning rate closer to 0 and check for the cost function, loss and accuracy. Say you chose 0.001 learning rate for a model, then try using 0.003 learning rate and check for the accuracy, cost function and loss.
running few epochs will not give the precise accuracy for model training and it wouldn’t be a precise method of checking if the model is proper as usually in the beginning if you notice the cost of learning first increases and then goes down after a point eventually reaching to minimum or closer to 0.
It is basically the criteria of choosing learning rate randomly rather than choosing 0. The rate of learning or speed at which the model learns is controlled by the hyperparameter. It regulates the amount of allocated error with which the model’s weights are updated each time they are updated , such as at the end of each batch of training instances.
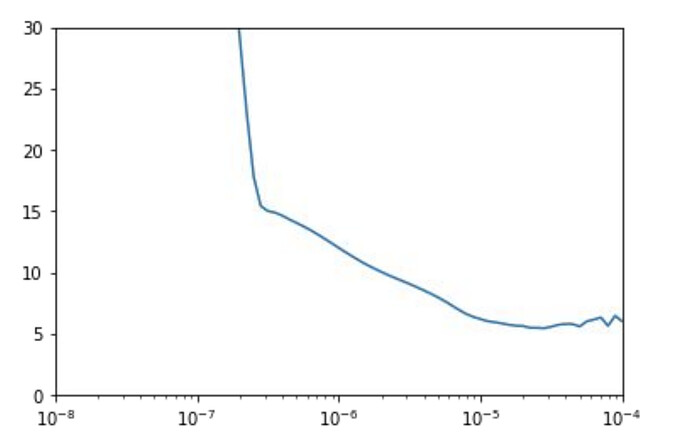
Please refer this Question regarding learning rate graph from W2 logistic regression lab - #3 by Deepti_Prasad
Hope it clarifies your doubt, otherwise do let us know. Keep Learning !!
Regards
DP
Hi DP, thanks for your reply.
Allow me to rephrase my last question above: “Would it be more appropriate to run 100 epochs for one specific learning rate and (while resetting parameters) iterate to get the loss after each of this process?”
I take from your answer that this is good approach. But I am still confused as to how does a one single run of 100 epochs is good enough when we use a ‘LearningRateScheduler’ as callback after each epoch.
When using the ‘LearningRateScheduler’ as callback after each epoch the loss for each epoch (with a new learning rate) is being impacted by the parameters that have been learnt by the NN with those previously tried learning rates in previous epochs. Hence, using this approach to select a learning rate to use seems at least questionable. (?)
Hi Rodolfo,
I understood your question. you basically stating when the model has already learnt about neural network n number of times how does selecting or differentiating learning rate to choose an appropriate learning rate is justified?
You need to understand in model training the inputs, or parameters are always defined at the beginning which can never be changed for one round of epoch training like you mentioned 100 epochs, then when you want to change the learning rate you can always change the parameters to get a better model training based on the requirement of your desired accuracy.
For example you want to climb on a mountain top (this concept is totally theoretical), so you climbed the way without knowing how to reach and you took say 40 minutes but when you reached on top, you discovered there is an easier way going up and down the cliff which is less lethargic and time saving, so eventually you start choosing that way for better saving time and energy, and having a joyful experience.
So the main criteria here you need to understanding in defining or choosing an appropriate learning rate, one doesn’t look only at learning rate, it is combination of choosing the most appropriate learning rate based on the parameters available (which you can change based on your requirement), which can reduce the cost function and if the gradient descent has convergence. You can always change the parameters w and b to get a reduce J(w,b).
Did you notice the below image, I shared the link in the previous reply
Regards
DP
Hi Rodolfo,
I was having the same questions as you. My interpretation of why increasing the step size and choosing the one with the minimum cost value is a valid approach is that, if you are relatively near the minimum making a big step toward it that still reduces the cost function, means that you were justified to take that big step and not a bunch of small ones. If that step would have been to big, you would overshoot and the cost function would increase, as we see happens when we go around 5*10**-4.
Best Regards,
Rok