Hello,
I have a little bit of trouble understanding what the ‘d’ means/is standing for in the notation of derivatives. It is somehow confusing me, because I could not explain it´s behaviour with my current understanding of maths (it doesn´t seem to be a variable nor a function).
I´m wondering how d affects the term that it´s standing in front of.
I would really appreciate if someone has a good explanation for this!
Hi,
The derivates in the courses are the derivates regarding the cost J.
Namely when you see dA for example, you should understand it as dJ/dA. That’s for notation simplicity.
If you’re not familiar with the ‘d’ notation, which is more commonly used in physics, a simple way would be to consider the equation:
f(x) = w.x + b
the linear regression function (in the courses: y = w.x + b)
the notation ‘dx’ in this case would represent the derivate of f regarding x.
which means dx = f’ = df/dx
Thanks for your reply!
I probably should have made my question more clear.
You seem to describe the naming convention of code variables that store the derivates of i.e. the function J(x) in regard to it´s variable x (would be variable ‘dx’).
I´m rather struggling with this here:
df/dx
For me this notation seems like you´re deviding the derivate of the function f by the derivate of the number x. But this doesn´t make sense because there´s no derivate of a number (dx).
Also sometimes you see this notation of the same thing:
(d/dx)*f(x)
This seems to suggest d to be a variable, independent of any term coming directly after it (as it does in df/dx). So it could be written like this:
d = ?
What would that be? Or what different meaning has d in a formula?
Greetings!
‘d’ is not a variable or rather it is not a thing as its own.
I believe a more correct notation to what you mentioned would be (df/dx)(x)
Well, if you really want to give a meaning to ‘d’, it’s very close to the notion of delta, namely a very small variation. ‘d’ is just the limit case.

That is basically the definition of derivatives
in the equation above, you can see delta(x) as x+h-x, and delta(f) as f(x+h)-f(x), for h infinitely small.
1 Like
df/dx is the same thing as (d/dx)f(x). Basically if f is a function of x, you’re taking a ratio of the change in f to the change in x, given that the latter is an infinitesimally small quantity. The ‘d’ that is used while writing the notation represents the Greek letter Δ (Delta), which is commonly used to show change in a quantity in physics and math. Andrew Ng has explained it very well in the course videos.
So basically dx would mean the change in x, df(x) would mean the change in f(x), and df(x)/dx as a whole is called the derivative of f(x) with respect to x. And of course, in the course the instructors have adopted the notation that dx represents df(x)/dx, however outside the context of this course dx would simply mean change in x.
Hope that helps 
1 Like
Thanks for the answers, they helped a lot!
I now understand the df/dx thing as somehow the ‘name’ of a function that represents the derivative of f with respect to it´s variable x.
This name (df/dx) is not directly a calculation (even if the notation seems to suggest this).
As you can see the function f isn´t given a parameter in this notation, therefore it doesn´t return anything you could calculate with. The f is just included in the notation to tell the derivative function (df/dx) that we want it to be the ‘derivative of the function f’.
Same is with the x. It is included to tell the derivative function that we want it to be ‘with respect to the functions variable x’, so the x isn´t a placeholder for some value but just a name.
So when writing (df/dx) (x) you can replace the x with some number and you get back the ‘derivative of the function f’ ‘with respect to the functions variable x’ at the place of your number.
The notation with the d and the fraction is hinting at what the function does internally:
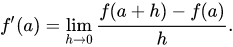
This is a different notation but f’(a) just stands for (df/da)(a). The function calculates the difference of f´s value (df) when shifting ‘a’ a little bit (by h) devided by the difference that a was shifted (da) by, which is the same as h.
This is my understanding of it, I hope it is somehow describing the question correctly, if not i´d be happy about some correcting hints.
Your understanding is absolutely correct. I am probably being pedantic here, but:
The difference in f’s value is df. d by itself doesn’t have much meaning, but suffixed by some other variable, df shows the change in f.
Since you seem unfamiliar with calculus, I would recommend you to take a basic course in it. There are many available on Coursera, and much more excellent content on YT, but I would suggest you check out 3blue1brown’s playlist on the essence of calculus. He gives a very intuitive way to understand differentials and integrals, and I have no doubt you will find this knowledge very useful in any technical field.
1 Like
I updated the post, hopefully in accordance with your suggestion.
Actually, I already started watching this great playlist and will abolutely continue watching it till the end in hope of getting a better insight to the topic!
Thanks again for taking the time to help me! 

1 Like


