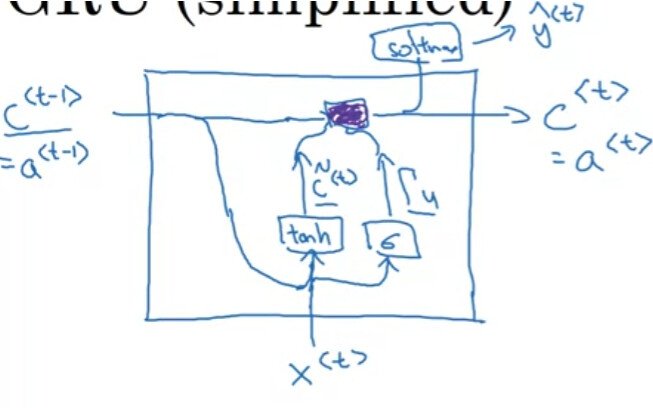
Like the picture shown, why the softmax use the c instead of the c~ to predict the result? If the gamma in c is 0, then the X will not be used to predict the result. In my opinion, should’t the predict result are affected by the x and c?
1 Like
Here is the flow in GRU.
As you see, the input to Softmax is c^{<t>}, which consists of two key terms, \tilde{c}^{<t>} and c^{<t-1>}. The point here is how to “balance” old information, c^{<t-1>}, and "new information,\tilde{c}^{<t>}. And, the update gate has that responsibility, and generates “\Gamma_u” for that purpose.
Think about a sentence. To generate a next word, sometimes an old information is important, but sometimes, only the last input should be referred.
So, \Gamma_u =0 is a valid option, but not sure it will be exact 0 or close to 0 in the real world.
And, you are very close.
If the gamma in c is 0, then the X will not be used to predict the result.
That’s the purpose of \Gamma_u, but the objective is as you wrote,
In my opinion, should’t the predict result are affected by the x and c?
GRU uses \Gamma_u for balancing.
Hope this helps.
1 Like
That make sense thanks.