Can someone please help me understand how the derivative of f^-1(y) turns from 1/f’(x) to 1/f’(f^-1(y)) in this explanation? I have spent a lot of time trying to figure this out. To me, f’(x) should be e(x) because the derivative of e(x) is just e(x) - so given that, I do not see any equaility between e(x) and f^-1(y), which is clearly log(y). We seem to be suggesing that log(y) = e(x). Either this is a mistake in the diagrams and the video lecture, or I am missing something.
Before:
After:
Hey @Hartej_Dhiman,
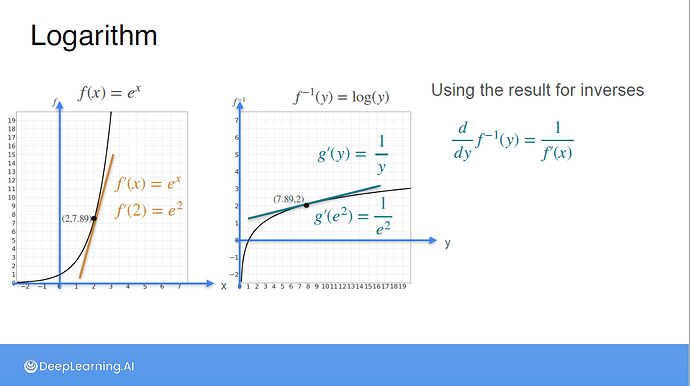
I really appreciate your post. It’s something even I got confused in when I was going over the content myself. Let us start from the foundation. First, we will borrow the result from the lecture video “The inverse function and it’s derivative”, i.e.,
If you are confused with this much, then I recommend you to watch this lecture video once again, since I have just stated the result from the lecture video. Now, let’s move on to understand how we can obtain the derivative of log from this property. In the video “The derivative of log(x)”, it was established that log(x) is the inverse of e^x, i.e., log(e^x) = x.
So, let’s say that g(y) = log(y) and f(x) = e^x, where f and g are inverse of each other. We invoke the result from before:
Now, note that from the result, we also have y = f(x) = e^x. So, we substitute e^x with y on the RHS on the equation, so that we can get an expression for g'(y) in terms of y. So, we have:
Voila, we have the derivative of log(y) or log(x) 
Now, let’s go ahead, and break down your thoughts on this as well.
I guess this is very easy to understand. Since we have y = f(x), it means, we can rewrite this as x = f^{-1}(y), and now, we have simply substituted x with f^{-1}(y), in the above equation.
You are correct on this.
You are mistaken on this. One is not supposed to see any equality between these 2. The result states that \frac{1}{e^x} is equal to the derivative of log(y), as I have mentioned above.
Let us know if you still have any confusion on this, and we will be more than happy to help you out.
Cheers,
Elemento
Hi, @Elemento, while I fully appreciate your response and the proof does make sense to me, where in Mr. Serrano’s slides/video lecture is it stated that y = f(x)? It sounds like he is implying that y = f(x). When you are in the business of educating masses of students on the fundamentals of something, you should not be implying something that the proof hinges on. To me, it appears Mr. Serrano is leaving the curriculum support staff to defend his iffy content by providing clarifications to students who come here after struggling to understand something that could have been relatively straightforward.
Besides all of that, I think a much better proof that f’ln(x) = 1/x is by using the formal definition of derivative as a limit of something → 0.
I should also mention that here, we are dealing with Natural Log, which should technically be written as ln(x), but I can live with that.
A really clear proof is demonstrated in this (free of charge) video:
Lastly, it is astounding to me that I have found, repeatedly, that free content out there is superior to the shortcuts taken in Coursera explanations, considering Coursera is $50 a month, per course, per month. (maybe that qualifies as a great example of cost increases exponentially)
Overall, I feel like I am learning about some critical fundamentals, but I can’t honestly fully credit the Coursera curriculum or material for that. I feel most of my learning is coming from external supplemental material.
Hey @Hartej_Dhiman,
First of all, thanks a lot for your feedback, and for sharing the video. It was really intriguing to look at the derivation from other perspectives 
I do agree with this; I don’t recall any explicit mention in the lecture videos of y = f(x).
But to me, it was trivial to understand this, once I went through the lecture video. I could see this at 2 places at least in the video “The inverse function and its derivative”:
g(f(x)) = x, so when afterwards, he made a plot of g(y), it was trivial to understand that y = f(x) here.f(x), and hence, naturally in the right plot, the horizontal axis should be f(x) too, which he represents as y, and therefore, y = f(x).Just to tell you my opinion regarding this, Coursera never helps me to master any topic, or to gain a deep understanding of any topic, for that matter. But what it does is that it helps me to begin on the path of understanding a new topic by providing a structured road-map, and whenever I am stuck, I know what to look for, and at times, even where to look for.
As to this, once again, I do agree. Let me tag in a staff member here, so that your feedback can be taken forward, and incorporated in future revisions of the course.
Hey @lucas.coutinho, can you please take a note of this thread, and pass this feedback along. Thanks in advance.
Cheers,
Elemento
Thanks, @elemento sincerely for your objective evaluation of my comments, and for all your help. I think you’re the best I have seen from DLAI Support. Cheers 
Hey @Hartej_Dhiman,
I am glad I could help you out 
As to this, just a small typo. The entire DLAI community stands apart from Coursera and it’s support team, and to quote J.K. Rowling, “Help is always given at DLAI to those who ask for it!” 
Cheers,
Elemento
I stand corrected. I owe all the great support to the DLAI community.