The inverse of log(x)

Course Q&A Math for Machine Learning Calculus for Machine Learning and Data Science
1

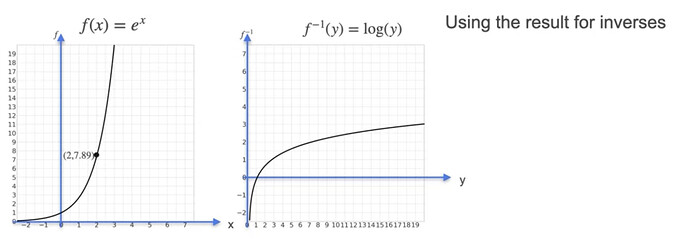
Hello, I am a bit confused with why the inverse in this lesson is stated as ƒ-1(y) = log(y) in the video, “The Derivative of Log(x)”.

I did a lot of reading online, and the inverse for e^x is always listed as y =ln(x) or f^-1(x) = ln(x) … never as log(y). Is this a mistake, or do these essentially mean the same thing? Maybe the video is showing a reflection of ln(x)?

image
image1904×660 93 KB

Also, the video keeps referring to e^2 as 7.89, but I believe it should be 7.389 (I reported the issue, and didn’t hear anything back).

Thanks in advance for any guidance on this :slight_smile:

2

The notation in the ML world is different than in math. Here log(z) always refers to the natural logarithm, so that is exactly equivalent to ln(z) in normal math notation.

I’m not sure historically how this difference came about, but one theory would be that in MATLAB (which was one of the primary languages for doing ML work in the early days), the natural log function is log(z) and log base 10 is log10(z).

Note that python and numpy do it that same way: the functions are np.log, np.log10 and np.log2.

1 Like
3

Oh, sorry, forgot to mention that you are correct about e^2, of course. I’ll report the bug.

4

Apologies for the slow reply - just wanted to say thank you! It helped me a lot :slight_smile:

1 Like
5

Hello @pinkninja,
I am delighted to answer your query even though I am a fellow learner.
Here in the video instructor took the variable for inverse function as ‘y’ so, f^-1(y) = ln (y).
It is same as f^-1(x) = ln(x) which is also same as g^-1(y) = ln(y).
Hope I answered correctly.