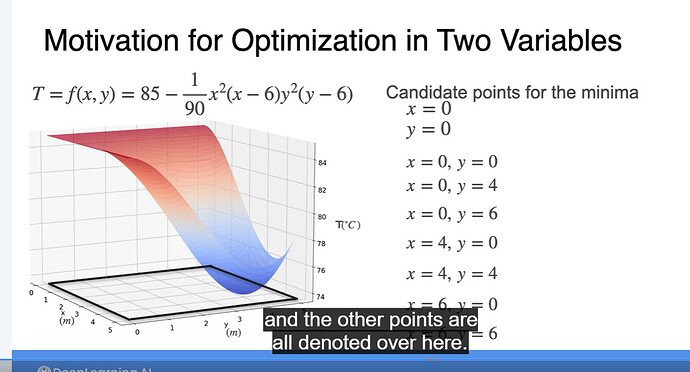
In order to make both derivative =0, when x =0, y can take anything and both equations are still 0. so why in the x,y pair, y can only take on 0,4,6 instead of any value?
Just because both derivatives are zero does not mean it’s a global minimum. The line where x = 0 is at the upper left and every point on that edge is a local maximum, right? So that solution does not work if the goal is to find the minimum.
We can see the graph, so we don’t need to compute to know where the global minimum is. But without the graph, how do we know what y value should be when x=0? And do you mean the candicate points for the minima on the first image does not cover the whole pair possibilities?
If you don’t have the ability to see from the graph, you just have to try all possible combinations to see which one gives the minimum.
Well, there are more sophisticated methods as well: if you compute the second derivatives, then you could use those to distinguish between local minima, local maxima and saddle points. It’s been a while since I took this course, so I don’t remember whether he covers those methods here.